大問1=計算問題を中心として小問が7題
大問1は基本的に全問正解すること。
そのうえ、いかに速く、負担を少なく計算するかが課題です。
動画解説はこちら

大問2=平均、連立方程式、確率の基礎問題
大問2も基本的な問題なので、できるだけ速く、ミスなく解き進めたいところです。
(1)の解説はこちら
(2)の解説はこちら
(3)の解説はこちら

大問3=2次関数のグラフと等積変形
放物線と直線が交差して、四角形や三角形とからませる典型的な問題。
後半では等積変形も利用します。

前半の(1)、(2)は二次関数のグラフのお決まりのパターン。素早く解きましょう。
(1)の動画解説はこちら
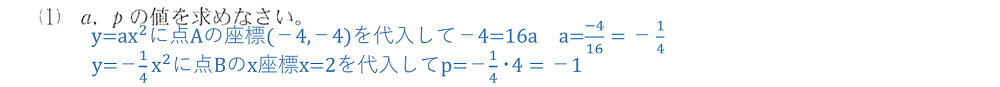
(a、p各1点)
(2)の動画解説はこちら
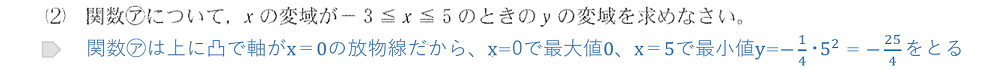
(2点)xの変域が-3≦x≦5で、x=0を含んでいることに注意。
一般的にこのような場合、x=0で最大値か最小値としてy=0をとります。
(3)の動画解説はこちら

(2点)2点を通る直線の式の求め方は、連立方程式を使わずにまず傾きを求めてから切片bを求めるようにしましょう。
「傾き」をイメージすることが極めて重要です。
(4)の動画解説はこちら

(2点)点Dの座標を(0,t)と文字を使って表すところがポイント。
点Cが放物線上の点であることと、線分ABと線分DCが平行で長さが等しいことから、点Cの座標を2通りに表します。

(5)の動画解説はこちら

(2点)(4)で点Dの座標が決まるので△AEDの面積が求められます。
ここで△CDFのおおよその形を想像しながら等積変形を思い出しましょう。
大問4=作図、空間図形(三角錐)
大問4は底角が30°の二等辺三角形の作図と、三角錐の体積と辺の長さを求める問題です。

(3点)二等辺三角形の作図
(1)の動画解説はこちら
(2)①の動画解説はこちら
(2)②の動画解説はこちら

(2点)①では三角錐の底面△GEFの面積を、点Gが辺DFの中点であることを使ってできるだけ簡単に求めましょう。
(2点)②では△BGEが直角三角形であることから、三平方の定理を利用します。
大問5=図形の証明問題、計量問題
証明、計量問題ですが、例年と同じように後半は難しいです。

(1)の動画解説はこちら
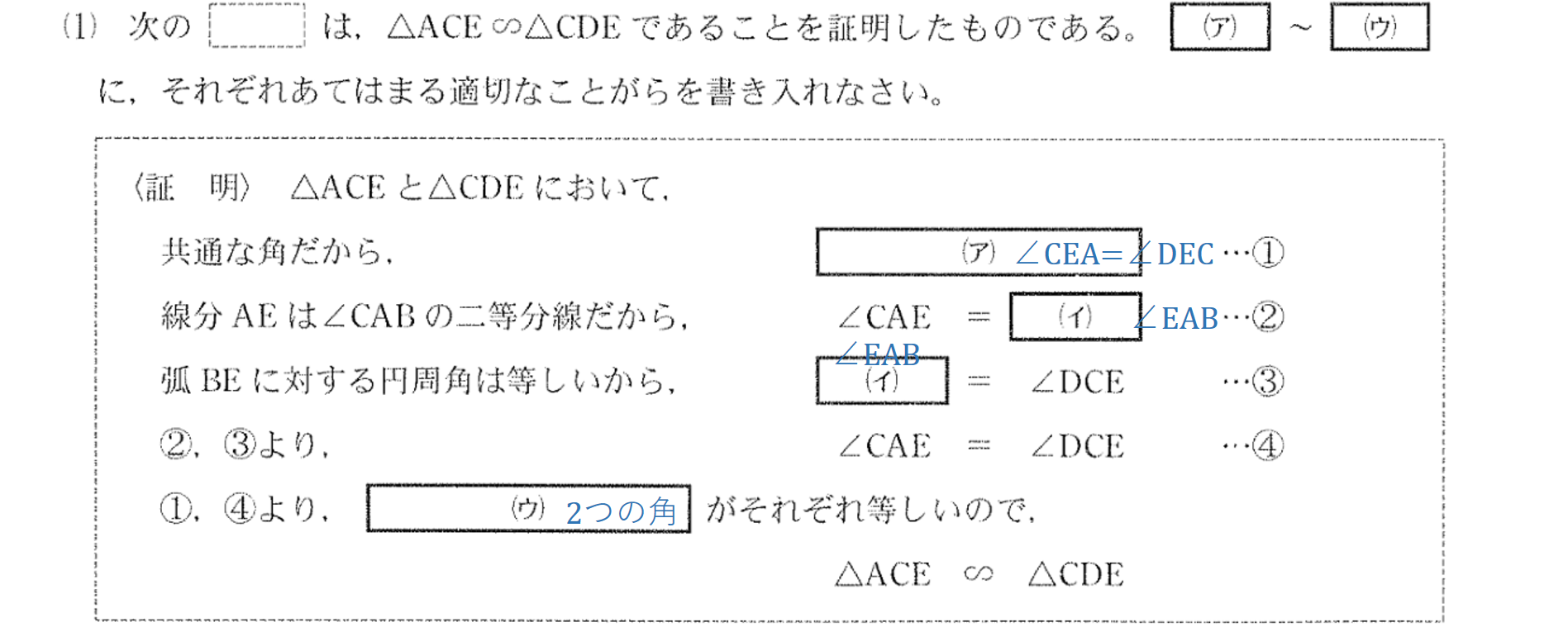
(ア、イ、ウ、各1点)誘導に乗って素直に考えましょう。
(2)の動画解説はこちら


(4点)対頂角が等しいことは容易に気がつきますが、直角は直径と接線の関係、直径と円周角の関係から説明します。
1組の辺が等しいことを△GADが二等辺三角形になることから説明する必要があります。
ここがクリアできるかどうかがこの問題のポイントです。

(3)①の動画解説はこちら
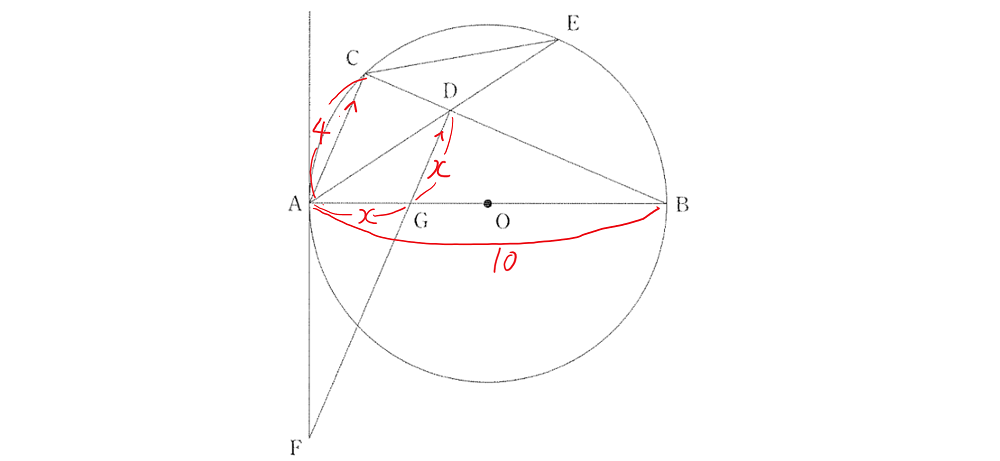
(2点)△GADが二等辺三角形であることは(2)でわかっているのですが、AG=GDを△CABと△DGBの相似比の式に利用するところが難しいです。

(3)②の動画解説はこちら

(2点)問題はたった1行だけですが、内容はかなり難しくて、しかも面倒くさいです。
それでいて配点は2点だけですから、ほとんどの場合深入りしないほうが無難です。
まずは「これまでの問題をしっかり見直して、それでも時間が余っていれば挑戦する」ぐらいでいいでしょう。








コメントを残す