◎今年も「易しめの問題を数多く」という方針が感じられて、取り組みやすいテストだと思います。
大問1は計算主体の小問集合
大問2は関数、図形に関する小問集合
大問3は袋からカードを取り出す場合の数と折り紙を題材とした図形問題の2問
大問4は放物線と直線を交差させて、三角形の面積、等積変形、三角形の面積の2等分まで含んだ総合的な問題

(3),(7)は辺々2乗して整理する。
(6)平均の問題は合計点で考える。

(3)Xの定義域がX=0を含んでいるので最小値に注意。
(4)一般的に「矢じり型」では∠COE=∠CAE+∠ACO+∠AEOが成り立つ。

(5)△AECと△DBFのそれぞれで中点連結定理を使う。

(3)0点で引き分け0(3)3点で同点になる場合、Aの1つの引き方に対してBの引き方が2つある点に注意。
0点で引き分けの場合 A(-2,2)B(-1,1)、A(-1,1)B(-2,2)
1点で引き分けの場合 A(-1,2)B(-2,3)、A(-2,3)B(-1,2)
2点で引き分けの場合 A(-2,4)B(-1,3)、A(-1,3)B(-2,4)
3点で引き分けの場合 A(-2,5)B(-1,4)、A(-2,5)B(1,2)、A(-1,4)B(-2,5)、A(-1,4)B(1,2)、A(1,2)B(-1,4)、A(1,2)B(-2,5)
4点で引き分けの場合 A(-1,5)B(1,3)、A(1,3)B(-1,5)
5点で引き分けの場合 A(1,4)B(2,3)、A(2,3)B(1,4)
6点で引き分けの場合 A(1,5)B(2,4)、A(2,4)B(1,5)
7点で引き分けの場合 A(2,5)B(3,4)、A(3,4)B(2,5)
(4)Aが3点になる場合は3通りあることに注意。
Aが(-2,5)の場合 Bは(1,3)、(1,4)、(2,3)、(2,4)、(3,4)
Aが(-1,4)の場合 Bは(1,3)、(1,5)、(2,3)、(2,5)、(3,5)
Aが(1,2)の場合 Bは(-1,5)、(3,4)、(3,5)、(4,5)
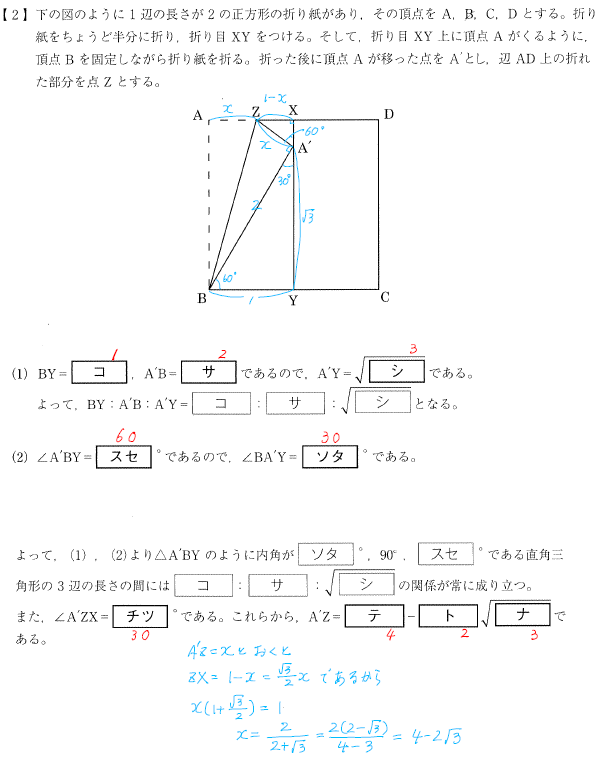
(1)三平方の定理で計算する。
(2)△A’BCは正三角形になる。
△ZA’X∽△A’BYより、辺の長さの比で関係式を導く。
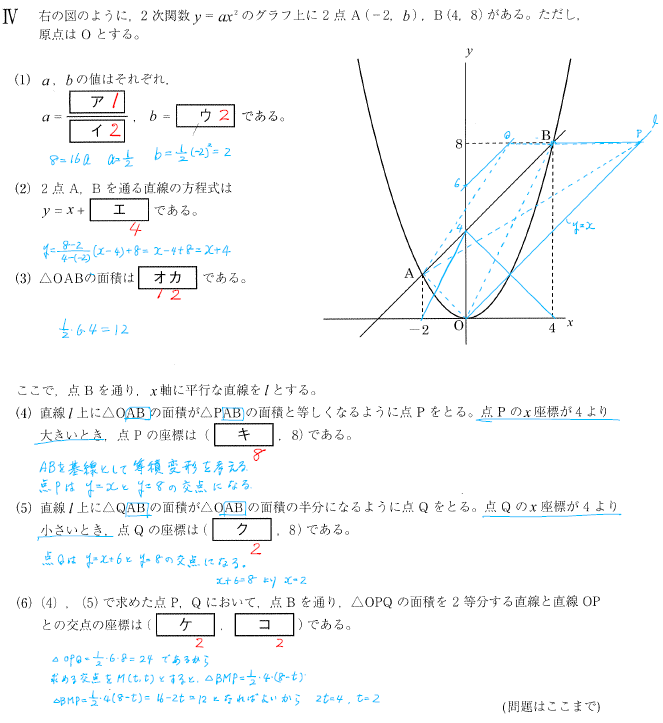
(2)2点を通る直線の方程式を求める計算は超重要。傾きを求めてから切片を計算すること。
(3)等積変形をすれば簡単に計算できる。
(4),(5)等積変形で考える。x座標が4より大きいか、小さいかに気をつける。







コメントを残す